The Collatz sequence for a whole number n is generated by iterating:

\[a_n = \begin{cases} \frac{1}{2} a_{n-1} & \text{if $a_{n-1}$ is even} \\ 3 a_{n-1} + 1 & \text{if $a_{n-1}$ is odd} \end{cases}\]

The Collatz conjecture states that this sequence always terminates at 1. The Wikipedia entry has a graph by Jon McLoone, Director at Wolfram Research and all-around interesting person. I thought that was cool and wanted to make my own, so here’s what I came up with:

collatz graph

Also, check out the humungo version and the source that generated it using pygraphviz and GraphViz.

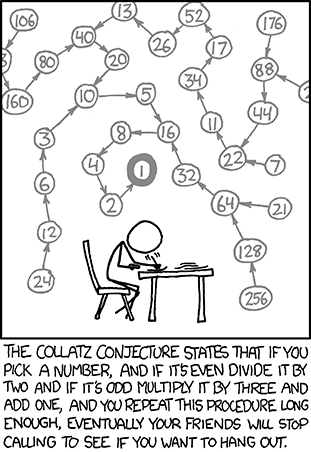
xkcd.com/710

Why does this work? Thinking in terms of prime factors, the half rule removes factors of 2. The triple-plus-one rule increases the next value, but makes sure there’s always at least one factor of 2 to remove. For the cases where triple-plus-one yields more than one factor of 2, we’ve made a profit. After removing twos by halving, the remaining factors are less than the odd number we tripled-plus-one.

Longer paths tend to be chock-full of primes, like the sequence for 89 in which every odd number is a prime. Does knowing that a number is of the form (3n+1)/2 tell us anything about its prime factors? Does it help to remember that all primes are either 6n+1 or 6n-1?

I dunno, but the Collatz conjecture remains unproven for a reason.